PID控制机制

PID控制和温度控制

在这里，我们将解释配备 PID 控制算法的温度控制器的实际运行情况。控制是指“对某事物进行必要的操作，以使其符合特定的目的。”换句话说，在温度控制的情况下，这意味着“添加操作以使温度目标值和测量点的温度变得相等”（图1）。图中虚线部分是对应温度控制器功能的框图，控制部分C对应带有PID控制算法的部分。

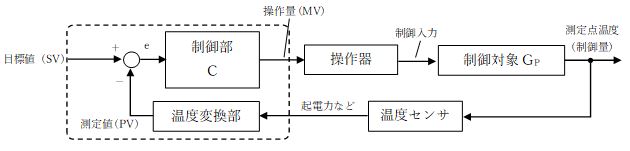
图1：温度控制概念图

2.1. PID控制的基本公式

PID控制的基本公式是：比例作用（P作用）与偏差e成正比（=SV-PV），积分作用（I作用）与偏差e的积分成正比，偏差e的导数为。表示为与（方程（1））成比例的微分作用（D作用）的总和。

基本上可以设置三个参数：比例增益 (K P )、积分时间 (T I ) 和微分时间 (T D )。然而，对于温度控制器，通常不直接指定比例增益，而是指定比例带 P B = 100 / K P [℃]（或 [%]），它是比例增益 (K P )的倒数。 是。从等式（1）右侧第一项开始，依次显示比例项（P 运算输出）、积分项（I 运算输出）和微分项（D 运算输出）。

2.2. PID控制算法的含义

当人类做出决定时，他们在得出结论之前会考虑三个因素：过去、现在和未来。 PID控制算法也可以解释为根据这三个要素确定运算量，例如“过去⇒I动作”、“当前⇒P动作”和“未来⇒D动作”。

2.3. 关于P运算和偏移

2.3.1. P 操作

P运算由式(2)表示，输出与电流偏差e成比例的输出。

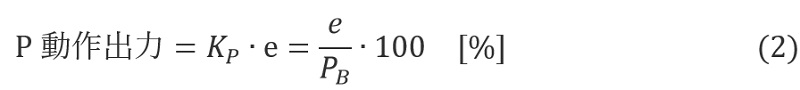
可见，当比例增益K P增大时，即使偏差e相同，P运算输出也变大。然而，实际上，存在物理限制，因此操作变量MV只能在有限范围内移动，例如0至100[%]。例如，比例带P B =30[℃]，目标值SV=100[℃]，测量值PV=40[℃]，

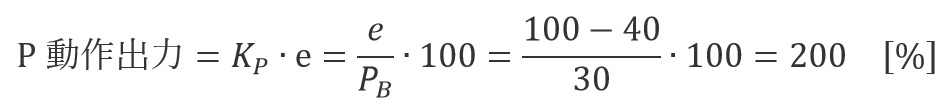
因此，操作变量MV应为200[%]，但实际上仅达到100[%]（图2（a））。

尽管该操作简单且易于理解，但单独的 P 操作存在一个问题，即即使经过足够的时间后，偏移（稳态偏差）仍然存在（图 2（a））。增大比例增益K P会减小偏移，但PV 响应会变得更加振荡，如果进一步增大，将会出现持续振荡。如果K P设置为不振动，则始终会留下偏移，因此这就是P 操作的极限。

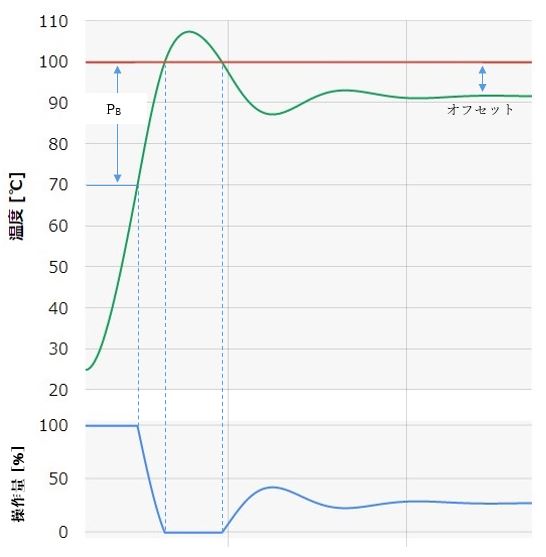
图2(a)：使用P运算的温度控制示例（比例带：30[℃]，SV：100[℃]）

2.3.2. 偏移量

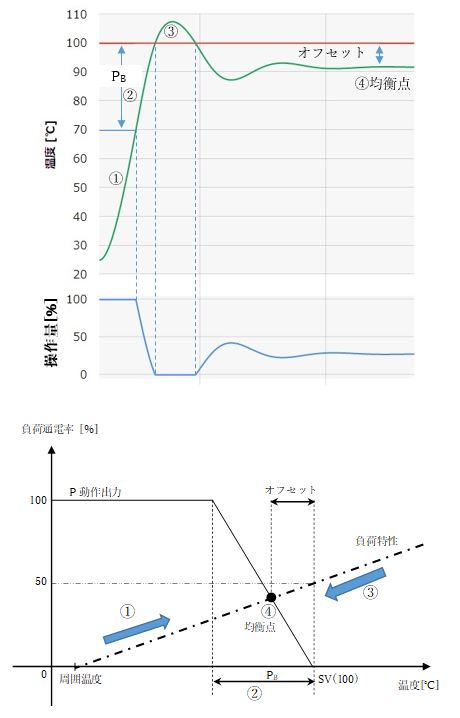
图2(b)：P动作输出及负载特性

当偏差e为0时，P运算输出为0[%]。这就是单独P运算时总是出现偏移的原因。例如，对于具有图2(b)所示的负载特性(*1)的控制对象，为了将PV稳定在SV=100[℃]，需要MV(操作量)为50[%]。

① 初始时，如果PV处于环境温度（25[℃]），则将输出相应的P运算输出=100[%]（输出上限值）。

② 在比例带内，P运算输出与偏差e成正比。 P 运行输出随着接近 SV 而减小，随着远离 SV 而增大。

③SV(100[℃])≤PV时，P运算输出为0[%](输出下限值)。从图2（b）的负载特性可以看出，PV逐渐试图降至环境温度。

④最终，PV稳定在P运行输出与负载特性之间的平衡点（图2（b）中的交点）。
在该平衡点处剩余的偏差称为偏移量。

为了消除偏移，需要在式(2)中添加50[%]的手动复位值(图2(c))，或者根据负载特性添加I运算。
(*1) 这里，负载特性定义为控制对象的温度达到稳定（热平衡）状态时的温度[℃]与此时的负载通电率[%]之间的关系。

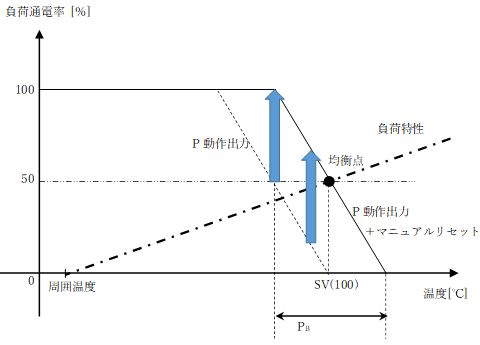
图2(c)：P运算输出及手动复位(50[%])

2.4. PI 运算和积分时间

将 I 运算输出添加到等式 (2) 中，得出 PI 运算的等式 (3)。

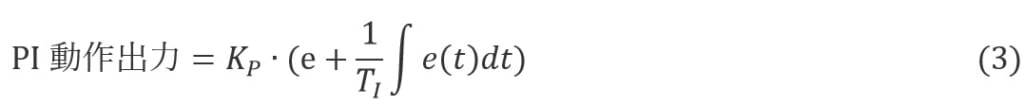
由于I-motion是过去偏差e的总和，因此可以看出，如果(e>0)，它会逐渐增加，如果(e<0)，它会逐渐减少。当I动作输出初始值为0且偏差一定时，t1时刻的P动作输出和I动作输出可用下式表示。

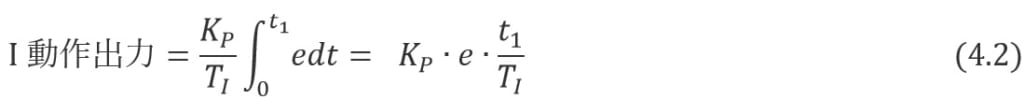
比较两个方程可以看出，当t 1 =T I时，P运算输出=I运算输出。由此，可以说“从输入一定的偏差到P动作输出与I动作输出相等的时间为积分时间TI”。 P 动作产生与偏差成比例的恒定输出，而只要偏差 e 不为零，I 动作就会继续增加（或减少）输出。因此，即使收敛速度根据积分时间TI而变化，偏移量最终也将变为0。这里重要的是，即使偏差e变为0，到该点为止的积分值也被保留。使用I运算输出，可以获得与自动修正手动复位值相同的效果。

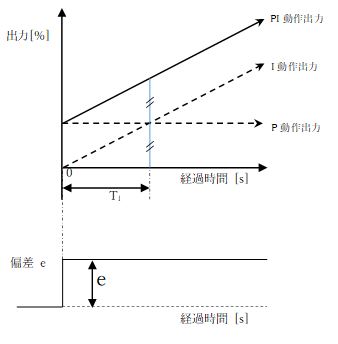
图3：PI运算的输出

2.5. PD 操作和微分时间

将与偏差 e 的微分成正比的 D 运算输出添加到等式 (2) 中，得出用于 PD 运算的等式 (5)。

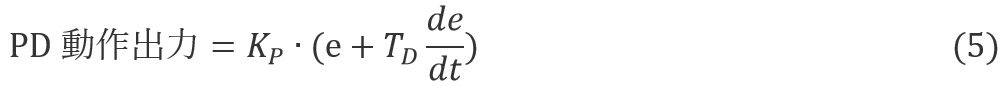
D运算给出与偏差e的微分值（变化率）成比例的输出，并抑制偏差的未来变化率。由于D作用会产生与速度变化方向相反的阻力，因此有时将其比作阻尼器。阻尼器也称为减震器（一种抑制振动的装置），是构成汽车、摩托车等悬架的部件之一。如果不这样做的话，车身的振动就无法被抑制，乘坐起来就会变得不舒服。 D 动作还可以抑制振动。例如，如果稳定在 PV = SV 的温度因干扰而突然下降（de/dt>0），则通过沿正方向输出 D 运算输出，可抑制因干扰而引起的变化。另外，当温度上升时（de/dt<0），通过向负方向输出 D 运算输出来抑制过度的温度上升（过冲）。如图4所示，当偏差以恒定速度增加时，D运算输出（D输出）的值保持恒定。当偏差一定时（变化率为零），D运算输出为零，因此无法消除偏移。

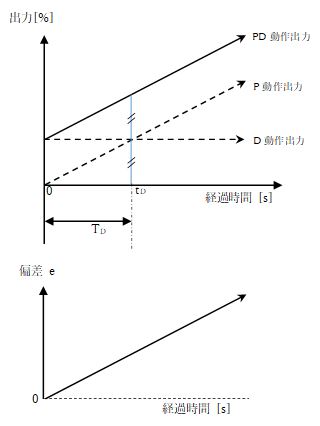
图 4：PD 操作的输出

微分时间TD被定义为当加上斜坡状偏差(以恒定斜率变化的偏差)时“直到(P运算输出)=(D运算输出)为止的时间”。[打开PID模拟器]

可以确认D运算输出是向阻尼振动方向输出。注意，在模拟器中，即使偏差恒定，D运算输出的值也不一定恒定。这是因为等式(5)中的算术表达式通常被称为“完全微分”，并且实际上并不实用。在模拟器中，偏差e经过一阶滞后滤波器处理，然后计算导数，这称为“不完全微分”。

三、结论

在这里，我们使用数学公式和模拟器解释了每个 PID 控制的基本操作。实际控制除了基本操作之外还需要各种巧思，但我们希望这个技术说明页面能够对您有所帮助。